Visualising brightness

Dr Alan D. Thompson left his position as Chairman of Mensa International's Gifted Families in 2020, after seeing the capabilities of GPT-3 outperforming his prodigy clients. (Read his 2020 paper, The New Irrelevance of Intelligence, and watch his 2021 presentation to the World Gifted Conference featuring Leta AI backed by GPT-3). Join subscribers from RAND, Pearson (Wechsler), Tesla, Microsoft, and Google AI for Dr Alan's monthly updates on integrated AI:
Get The Memo.

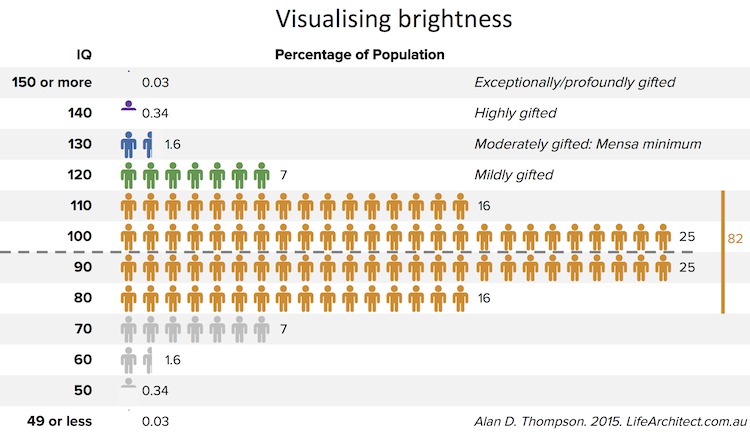
IQ chart

Download IQ chart (PDF – A4 printable)

This chart is also featured in the best-selling book, Bright (a copy of this book was even sent to the moon!).

To cite this chart: Thompson, A. D. (2016). Bright: Seeing superstars, listening to their worlds, and moving out of the way. Life Architect.

IQ mental age

Chronological & Mental Ages of Gifted Children
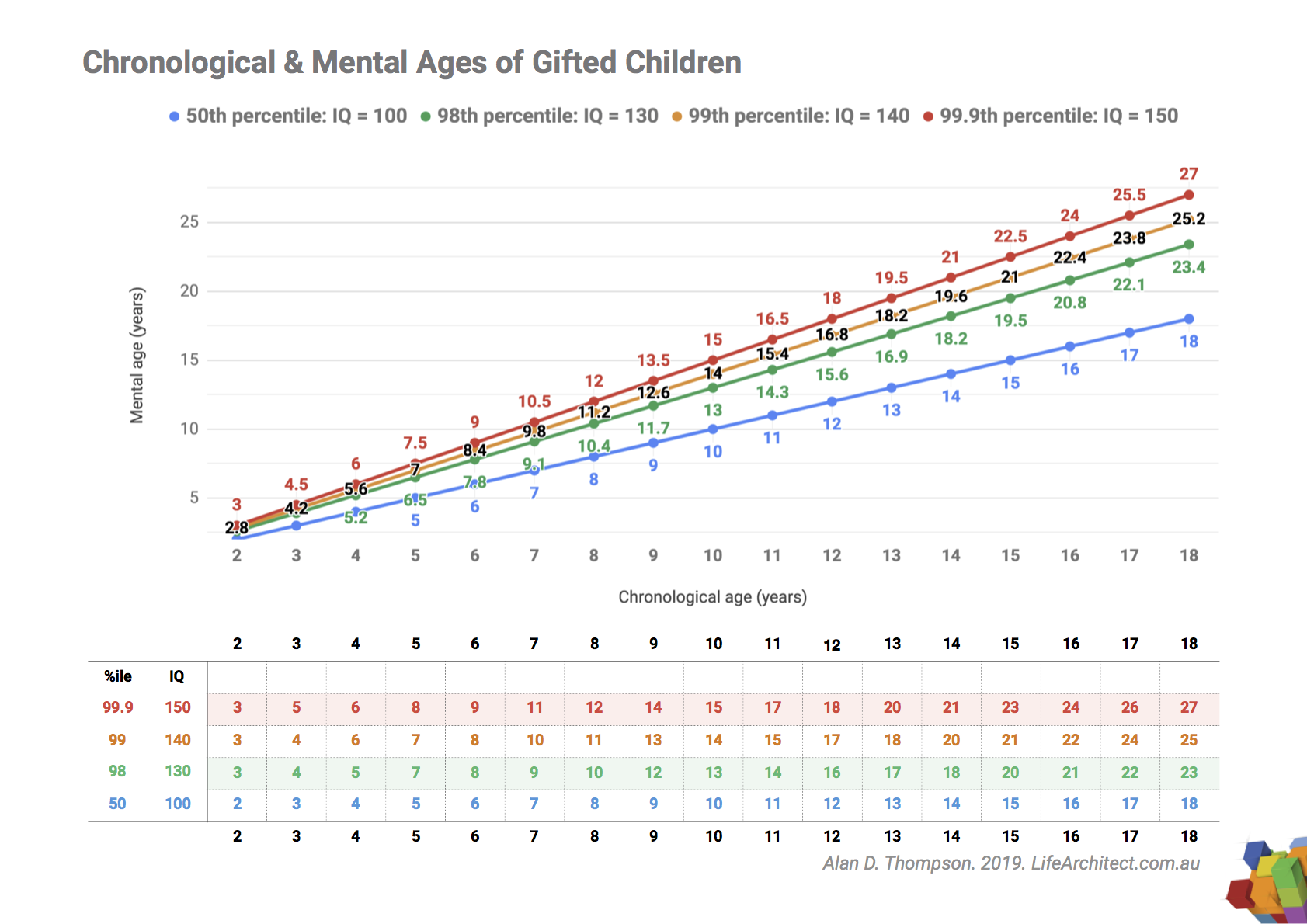Download Mental Ages of Gifted Children chart (PDF – A4 printable)

To cite this chart: Thompson, A. D. (2019). Chronological & Mental Ages of Gifted Children. Life Architect.

Summary IQ percentile and rarity

IQ table (uses 15SD as in Wechsler)
Most numbers have been rounded to nearest significant figure.

IQ Percentile Top % 1 in…
120 90.87 9.13 11
125 95.2 4.8 21
130 97.7 2.3 44
135 99 1 102
140 99.6 0.4 261
145 99.86 0.14 741
150 99.95 0.05 2,330
155 99.98 0.02 8,137
160 99.996 0.004 31,560
165 99.9992 0.0008 136,074
170 99.9998 0.0002 652,598
175 99.99997 0.00003 3.5 million
180 99.999995 0.000005 20.7 million
185 99.9999992 0.0000008 137 million
190 99.999999901 0.000000099 1 billion
195 99.99999998 0.00000002 8.3 billion
200 99.999999998 0.000000002 76 billion
IQ Percentile Top % 1 in…

Convert confidence interval to percentile and IQ score (Wechsler)

From the WISC-V technical report (August, 2015).

FSIQ Percentile
Rank		 90%
Confidence
Interval		 95%
Confidence
Interval
120 91 114-124 113-125
125 95 119-129 118-130
130 98 123-134 122-135
135 99 128-138 127-139
140 99.6 133-143 132-144
146 99.9 138-149 137-150
150 >99.9 142-153 141-154
155 >99.9 147-157 146-158
FSIQ Percentile
Rank		 90%
Confidence
Interval		 95%
Confidence
Interval

Show more detail for confidence interval to percentile and score

FSIQ Percentile
Rank		 90%
Confidence
Interval		 95%
Confidence
Interval
120 91 114-124 113-125
122 93 116-126 115-127
124 95 118-128 117-129
125 95 119-129 118-130
126 96 119-130 118-131
127 96 120-131 119-132
128 97 121-132 120-133
130 98 123-134 122-135
131 98 124-135 123-136
132 98 125-136 124-137
133 99 126-137 125-138
134 99 127-138 126-139
135 99 128-138 127-139
136 99 129-139 128-140
137 99 130-140 129-141
138 99 131-141 130-142
140 99.6 133-143 132-144
141 99.7 134-144 133-145
142 99.7 135-145 135-146
143 99.8 136-146 135-147
144 99.8 137-147 136-148
146 99.9 138-149 137-150
147 99.9 139-150 138-151
148 99.9 140-151 139-152
149 99.9 141-152 140-153
150 >99.9 142-153 141-154
151 >99.9 143-154 142-155
152 >99.9 144-155 143-156
153 >99.9 145-156 144-157
154 >99.9 146-157 145-158
155 >99.9 147-157 146-158
FSIQ Percentile
Rank		 90%
Confidence
Interval		 95%
Confidence
Interval

Full IQ Percentile and Rarity Chart

The table below is an archive backup of the IQ table originally published by Rodrigo de la Jara at iqcomparisonsite.com/iqtable.aspx [website is down as of Oct/2021].

These are IQs, their percentiles, and rarity on a 15 SD (e.g. Wechsler) and 16 SD (e.g. Stanford-Binet) scale. They were calculated using the NORMDIST function in Excel. The number of decimal places for the rarity was varied in the hope it might be useful. You can see why presently nobody should be able to get a deviation IQ higher than 195 (or 201 on the 16 SD scale). There are not enough people in the world to ‘beat’. Note that rarities given are of people that have a certain IQ or higher. Some people might find it more useful to know the rarity of people that have a certain IQ or lower. In that case use this example as a guide: If you want to know how many people have IQs of 84 or lower, look at the rarity of people that have an IQ of 116 or higher. (100 – 84 = 16. 100 + 16 = 116).

IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
202
99.9999999995%

190,057,377,928
99.9999999908%

10,881,440,294
201
99.9999999992%

119,937,672,336
99.9999999862%

7,252,401,045
200
99.9999999987%

76,017,176,740
99.9999999794%

4,852,159,346
199
99.9999999979%

48,390,420,202
99.9999999693%

3,258,706,819
198
99.9999999968%

30,938,221,975
99.9999999545%

2,196,908,409
197
99.9999999950%

19,866,426,228
99.9999999327%

1,486,736,899
196
99.9999999922%

12,812,462,045
99.9999999010%

1,009,976,678
195
99.9999999880%

8,299,126,114
99.9999998548%

688,720,101
194
99.9999999815%

5,399,067,340
99.9999997879%

471,441,334
193
99.9999999717%

3,527,693,270
99.9999996913%

323,940,499
192
99.9999999568%

2,314,980,850
99.9999995524%

223,436,817
191
99.9999999345%

1,525,765,721
99.9999993536%

154,701,783
190
99.9999999010%

1,009,976,678
99.9999990699%

107,519,234
189
99.9999998511%

671,455,130
99.9999986669%

75,011,253
188
99.9999997770%

448,336,263
99.9999980964%

52,530,944
187
99.9999996674%

300,656,786
99.9999972920%

36,927,646
186
99.9999995062%

202,496,482
99.9999961624%

26,057,620
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
185
99.9999992699%

136,975,305
99.9999945820%

18,457,107
184
99.9999989254%

93,056,001
99.9999923799%

13,123,126
183
99.9999984250%

63,492,548
99.9999893231%

9,366,012
182
99.9999977016%

43,508,721
99.9999850966%

6,709,882
181
99.9999966604%

29,943,596
99.9999792755%

4,825,216
180
99.9999951684%

20,696,863
99.9999712895%

3,483,046
179
99.9999930398%

14,367,357
99.9999603760%

2,523,720
178
99.9999900166%

10,016,587
99.9999455198%

1,835,530
177
99.9999857417%

7,013,455
99.9999253755%

1,340,043
176
99.9999797237%

4,931,877
99.9998981672%

982,001
175
99.9999712895%

3,483,046
99.9998615605%

722,337
174
99.9999595211%

2,470,424
99.9998125011%

533,337
173
99.9999431733%

1,759,737
99.9997470088%

395,271
172
99.9999205647%

1,258,887
99.9996599197%

294,048
171
99.9998894360%

904,454
99.9995445629%

219,569
170
99.9998467663%

652,598
99.9993923584%

164,571
169
99.9997885357%

472,893
99.9991923180%

123,811
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
168
99.9997094213%

344,141
99.9989304314%

93,496
167
99.9996024097%

251,515
99.9985889129%

70,867
166
99.9994583047%

184,606
99.9981452833%

53,917
165
99.9992651083%

136,074
99.9975712563%

41,174
164
99.9990072440%

100,730
99.9968313965%

31,560
163
99.9986645903%

74,883
99.9958815099%

24,281
162
99.9982112841%

55,906
99.9946667250%

18,750
161
99.9976142490%

41,916
99.9931192192%

14,533
160
99.9968313965%

31,560
99.9911555410%

11,307
159
99.9958094411%

23,863
99.9886734737%

8,829
158
99.9944812644%

18,120
99.9855483883%

6,920
157
99.9927627566%

13,817
99.9816290270%

5,443
156
99.9905490555%

10,581
99.9767326626%

4,298
155
99.9877101029%

8,137
99.9706395788%

3,406
154
99.9840854286%

6,284
99.9630868216%

2,709
153
99.9794780761%

4,873
99.9537611786%

2,163
152
99.9736475807%

3,795
99.9422913506%

1,733
151
99.9663019177%

2,968
99.9282392963%

1,394
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
150
99.9570883466%

2,330
99.9110907427%

1,125
149
99.9455830880%

1,838
99.8902448799%

911
148
99.9312797919%

1,455
99.8650032777%

741
147
99.9135767802%

1,157
99.8345580959%

604
146
99.8917630764%

924
99.7979796890%

495
145
99.8650032777%

741
99.7542037453%

407
144
99.8323213712%

596
99.7020181412%

336
143
99.7925836483%

482
99.6400497338%

278
142
99.7444809358%

391
99.5667513617%

231
141
99.6865104294%

319
99.4803893690%

192
140
99.6169574875%

261
99.3790320141%

161
139
99.5338778217%

215
99.2605391688%

135
138
99.4350805958%

177
99.1225537500%

114
137
99.3181130218%

147
98.9624953632%

96
136
99.1802471131%

122
98.7775566587%

82
135
99.0184693146%

102
98.5647029151%

70
134
98.8294737819%

85
98.3206753694%

60
133
98.6096601092%

72
98.0419987942%

51
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
132
98.3551363216%

61
97.7249937964%

44
131
98.0617279292%

52
97.3657942589%

38
130
97.7249937964%

44
96.9603702812%

33
129
97.3402495072%

38
96.5045568849%

29
128
96.9025987934%

32
95.9940886433%

25
127
96.4069734486%

28
95.4246402670%

22
126
95.8481819706%

24
94.7918730337%

19
125
95.2209669590%

21
94.0914867949%

17
124
94.5200710546%

18
93.3192771207%

15
123
93.7403109348%

16
92.4711969715%

13
122
92.8766585983%

14
91.5434221090%

12
121
91.9243288744%

12
90.5324192858%

11
120
90.8788718026%

11
89.4350160914%

9
119
89.7362682436%

10
88.2484711894%

9
118
88.4930268282%

9
86.9705435536%

8
117
87.1462801289%

8
85.5995592220%

7
116
85.6938777630%

7
84.1344740241%

6
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
115
84.1344740241%

6.30297414356
82.5749307167%

5.7388581000
114
82.4676075848%

5.70372814115
80.9213089868%

5.2414497373
113
80.6937708458%

5.17967538878
79.1747668425%

4.8018670064
112
78.8144666062%

4.72020213705
77.3372720270%

4.4125314534
111
76.8322499196%

4.31634490415
75.4116222443%

4.0669620824
110
74.7507532660%

3.96051419092
73.4014531849%

3.7596038872
109
72.5746935061%

3.64626736341
71.3112335745%

3.4856849025
108
70.3098594977%

3.36812148102
69.1462467364%

3.2410967685
107
67.9630797074%

3.12139865776
66.9125584538%

3.0222947235
106
65.5421696587%

2.90209798497
64.6169712244%

2.8262136810
105
63.0558595794%

2.70678919205
62.2669653200%

2.6501976543
104
60.5137031432%

2.53252414027
59.8706273779%

2.4919402788
103
57.9259687167%

2.37676298063
57.4365675495%

2.3494345790
102
55.3035150084%

2.23731239758
54.9738265155%

2.2209304558
101
52.6576534466%

2.11227383685
52.4917739192%

2.1048986302
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
100
49.9999999782%

1.99999999913
49.9999999782%

1.9999999991
99
47.3423465534%

1.89905917668
47.5082260808%

1.9050604034
98
44.6964849916%

1.80820333002
45.0261734845%

1.8190474693
97
42.0740312833%

1.72634143572
42.5634324505%

1.7410511155
96
39.4862968568%

1.65251826951
40.1293726221%

1.6702681161
95
36.9441404206%

1.58589543727
37.7330346800%

1.6059880144
94
34.4578303413%

1.52573527121
35.3830287756%

1.5475810473
93
32.0369202926%

1.47138711828
33.0874415462%

1.4944877660
92
29.6901405023%

1.42227563409
30.8537532636%

1.4462100941
91
27.4253064939%

1.37789076562
28.6887664255%

1.4023036061
90
25.2492467340%

1.33777916116
26.5985468151%

1.3623708477
89
23.1677500804%

1.30153679093
24.5883777557%

1.3260555472
88
21.1855333938%

1.26880259813
22.6627279730%

1.2930375921
87
19.3062291542%

1.23925302972
20.8252331575%

1.2630286642
86
17.5323924152%

1.21259732068
19.0786910132%

1.2357684429
85
15.8655259759%

1.18857342558
17.4250692833%

1.2110213007
84
14.3061222370%

1.16694450771
15.8655259759%

1.1885734256
83
12.8537198711%

1.14749590978
14.4004407780%

1.1682303146
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
82
11.5069731718%

1.13003254137
13.0294564464%

1.1498145914
81
10.2637317564%

1.11437662784
11.7515288106%

1.1331641064
80
9.1211281974%

1.10036577278
10.5649839086%

1.1181302847
79
8.0756711256%

1.08785129274
9.4675807142%

1.1045766896
78
7.1233414017%

1.07669678808
8.4565778910%

1.0923777776
77
6.2596890652%

1.06677691809
7.5288030285%

1.0814178174
76
5.4799289454%

1.05797635237
6.6807228793%

1.0715899553
75
4.7790330410%

1.05018887325
5.9085132051%

1.0627954070
74
4.1518180294%

1.04331660699
5.2081269663%

1.0549427583
73
3.5930265514%

1.03726936365
4.5753597330%

1.0479473616
72
3.0974012066%

1.03196406748
4.0059113567%

1.0417308129
71
2.6597504928%

1.02732426212
3.4954431151%

1.0362204981
70
2.2750062036%

1.02327967611
3.0396297188%

1.0313491967
69
1.9382720708%

1.01976583639
2.6342057411%

1.0270547348
68
1.6448636784%

1.01672371917
2.2750062036%

1.0232796761
67
1.3903398908%

1.01409942889
1.9580012058%

1.0199710454
66
1.1705262181%

1.01184389811
1.6793246306%

1.0170800762
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
65
0.9815306854%

1.00991260208
1.4352970849%

1.0145619785
64
0.8197528869%

1.00826528377
1.2224433413%

1.0123757196
63
0.6818869782%

1.006865686
1.0375046368%

1.0104838164
62
0.5649194042%

1.00568128874
0.8774462500%

1.0088521352
61
0.4661221783%

1.00468305052
0.7394608312%

1.0074496959
60
0.3830425125%

1.0038451537
0.6209679859%

1.0062484809
59
0.3134895706%

1.00314475418
0.5196106310%

1.0052232469
58
0.2555190642%

1.00256173637
0.4332486383%

1.0043513385
57
0.2074163517%

1.00207847461
0.3599502662%

1.0036125059
56
0.1676786288%

1.00167960262
0.2979818588%

1.0029887244
55
0.1349967223%

1.0013517921
0.2457962547%

1.0024640190
54
0.1082369236%

1.00108354203
0.2020203110%

1.0020242926
53
0.0864232198%

1.00086497974
0.1654419041%

1.0016571607
52
0.0687202081%

1.00068767465
0.1349967223%

1.0013517921
51
0.0544169120%

1.0005444654
0.1097551201%

1.0010987571
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
50
0.0429116534%

1.00042930075
0.0889092573%

1.0008898838
49
0.0336980823%

1.00033709442
0.0717607037%

1.0007181224
48
0.0263524193%

1.00026359366
0.0577086494%

1.0005774197
47
0.0205219239%

1.00020526136
0.0462388214%

1.0004626021
46
0.0159145714%

1.00015917105
0.0369131784%

1.0003692681
45
0.0122898971%

1.00012291408
0.0293604212%

1.0002936904
44
0.0094509445%

1.00009451838
0.0232673374%

1.0002327275
43
0.0072372434%

1.00007237767
0.0183709730%

1.0001837435
42
0.0055187356%

1.0000551904
0.0144516117%

1.0001445370
41
0.0041905589%

1.00004190735
0.0113265263%

1.0001132781
40
0.0031686035%

1.00003168704
0.0088444590%

1.0000884524
39
0.0023857510%

1.00002385808
0.0068807808%

1.0000688125
38
0.0017887159%

1.00001788748
0.0053332750%

1.0000533356
37
0.0013354097%

1.00001335428
0.0041184901%

1.0000411866
36
0.0009927560%

1.00000992766
0.0031686035%

1.0000316870
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
35
0.0007348917%

1.00000734897
0.0024287437%

1.0000242880
34
0.0005416953%

1.00000541698
0.0018547167%

1.0000185475
33
0.0003975903%

1.00000397592
0.0014110871%

1.0000141111
32
0.0002905787%

1.0000029058
0.0010695686%

1.0000106958
31
0.0002114643%

1.00000211465
0.0008076820%

1.0000080769
30
0.0001532337%

1.00000153234
0.0006076416%

1.0000060765
29
0.0001105640%

1.00000110564
0.0004554371%

1.0000045544
28
0.0000794353%

1.00000079435
0.0003400803%

1.0000034008
27
0.0000568267%

1.00000056827
0.0002529912%

1.0000025299
26
0.0000404789%

1.00000040479
0.0001874989%

1.0000018750
25
0.0000287105%

1.00000028711
0.0001384395%

1.0000013844
24
0.0000202763%

1.00000020276
0.0001018328%

1.0000010183
23
0.0000142583%

1.00000014258
0.0000746245%

1.0000007462
22
0.0000099834%

1.00000009983
0.0000544802%

1.0000005448
21
0.0000069602%

1.0000000696
0.0000396240%

1.0000003962
20
0.0000048317%

1.00000004832
0.0000287105%

1.0000002871
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
19
0.0000033396%

1.0000000334
0.0000207245%

1.0000002072
18
0.0000022984%

1.00000002298
0.0000149034%

1.0000001490
17
0.0000015750%

1.00000001575
0.0000106769%

1.0000001068
16
0.0000010746%

1.00000001075
0.0000076201%

1.0000000762
15
0.0000007301%

1.0000000073
0.0000054180%

1.0000000542
14
0.0000004938%

1.00000000494
0.0000038376%

1.0000000384
13
0.0000003326%

1.00000000333
0.0000027080%

1.0000000271
12
0.0000002230%

1.00000000223
0.0000019036%

1.0000000190
11
0.0000001489%

1.00000000149
0.0000013331%

1.0000000133
10
0.0000000990%

1.00000000099
0.0000009301%

1.0000000093
9
0.0000000655%

1.00000000066
0.0000006464%

1.0000000065
8
0.0000000432%

1.00000000043
0.0000004476%

1.0000000045
7
0.0000000283%

1.00000000028
0.0000003087%

1.0000000031
6
0.0000000185%

1.00000000019
0.0000002121%

1.0000000021
IQ
15 SD Percentile

Rarity: 1/X
16 SD Percentile

Rarity: 1/X
5
0.0000000120%

1.00000000012
0.0000001452%

1.0000000015
4
0.0000000078%

1.00000000008
0.0000000990%

1.0000000010
3
0.0000000050%

1.00000000005
0.0000000673%

1.0000000007
2
0.0000000032%

1.00000000003
0.0000000455%

1.0000000005
1
0.0000000021%

1.00000000002
0.0000000307%

1.0000000003

Get The Memo

by Dr Alan D. Thompson · Be inside the lightning-fast AI revolution.
Informs research at Apple, Google, Microsoft · Bestseller in 142 countries.
Artificial intelligence that matters, as it happens, in plain English.
Get The Memo.

Alan D. Thompson is a world expert in artificial intelligence, advising everyone from Apple to the US Government on integrated AI. Throughout Mensa International’s history, both Isaac Asimov and Alan held leadership roles, each exploring the frontier between human and artificial minds. His landmark analysis of post-2020 AI—from his widely-cited Models Table to his regular intelligence briefing The Memo—has shaped how governments and Fortune 500s approach artificial intelligence. With popular tools like the Declaration on AI Consciousness, and the ASI checklist, Alan continues to illuminate humanity’s AI evolution. Technical highlights.

This page last updated: 29/Nov/2023. https://lifearchitect.ai/visualising-brightness/↑